Consistency, Stability, Convergence

강좌: 기초 전산유체역학

Accuracy

Central Difference와 Upwind difference로 Wave equation을 해석한 기법의 정확도를 비교해보자. Taylor expansion을 이용하면 다음 관계를 얻을 수 있다.

\[ u_j^{n+1} = u_j^n + u_t \Delta t+ \frac{1}{2!} u_{tt} \Delta t^2 + \frac{1}{3!} u_{ttt} \Delta t^3 +... \]

\[ u_{j+1}^n = u_j^n + u_x \Delta x + \frac{1}{2!} u_{xx} \Delta x^2 + \frac{1}{3!} u_{xxx} \Delta x^3 +... \]

\[ u_{j-1}^n = u_j^n - u_x \Delta x + \frac{1}{2!} u_{xx} \Delta x^2 - \frac{1}{3!} u_{xxx} \Delta x^3 +... \]

Central scheme

First approach (Euler Explicit + Central difference) 에 이 결과를 적용하면 다음과 같다.

\[ u_t + a u_x = - \frac{\Delta t}{2} u_{tt} - \frac{a \Delta x^2}{6} u_{xxx} + O(\Delta t^2, \Delta x^3) = O(\Delta t, \Delta x^2) . \]

즉 시간에 대해서는 1차 정확도, 공간에 대해서는 2차 정확도를 갖는다.

Upwind scheme

Second approach (Euler Explicit + Upwind) 에 이 결과를 적용하면 다음과 같다.

\[ u_t + a u_x = - \frac{\Delta t}{2} u_{tt} + \frac{a \Delta x}{2} u_{xx} + O(\Delta t^2, \Delta x^2) = O(\Delta t, \Delta x) . \]

즉 시간과 공간에 대해 1차 정확도를 갖는다.

Consistency

\(\Delta x, \Delta t \rightarrow 0\) 일 때 차분식이 미분방정식과 같아지는 경우 이 기법이 Consistent 하다. Central scheme 과 Upwind scheme 모두 Consistent 하다.

Modified Equation

Upwind 또는 Central scheme의 경우 시간에 대한 미분 항 \(u_{tt}\) 을 다음과 같이 변형할 수 있다.

\[\begin{split} u_t = - au_x + O(\Delta t, \Delta x)\\ u_{tt} = -au_{xt} + O(\Delta t, \Delta x) \end{split}\]

여기서 \(u_{xt}=u_{tx}\) 이므로

\[ u_{tt} = -a u_{xt} = -a u_{tx} = -a \frac{\partial}{\partial x} \left ( -a u_x + O(\Delta t, \Delta x) \right ) = a^2 u_{xx} + O(\Delta t, \Delta x) \]

Upwind scheme에 이를 적용하면

\[ u_t + a u_x = \frac{a \Delta x}{2} u_{xx} \left ( -a \frac{\Delta t}{\Delta x} + 1 \right) + O(\Delta t^2, \Delta x^2, \Delta t \Delta x) = \frac{a \Delta x}{2} u_{xx} (1 - \nu) + O(\Delta t^2, \Delta x^2, \Delta t \Delta x) \]

\(\Delta x, \Delta t \rightarrow 0\) 이므로, 가장 크기가 큰 첫번째 오차항까지 생각하면, Upwind 기법은 다음과 같이 근사할 수 있다.

\[ u_t + a u_x = \epsilon u_{xx} \]

\(\epsilon > 0\) 일 때 \(\epsilon u_{xx}\) 은 작은 점성항과 같은 역활을 해서 시간이 지날수록 수치적인 해가 감쇄한다.

• (DIY) Central 기법에 대해 modified equation을 구해보시오.

Stability

Central scheme의 경우 정확도가 높음에도 시간이 지날 수록 해의 진폭이 점점 커져서 발산한다.

이는 수치 해석 기법의 안정성과 관계가 있다.

von Neumann Stability Analysis

선형 방정식이고, Periodic 경계 조건에 대해서 차분식의 수치 안정성은 von Neumann 안정성 분석으로 판단할 수 있다.

완전해를 \(D\) 라 했을 때 수치해 \(N\)은 다음과 같이 나타낼 수 있다.

\[ N = D + \epsilon. \]

여기서 \(\epsilon\) 은 round-off 에 의한 error 이다.

차분식에 이를 적용하면 오차에 대한 식을 구할 수 있다.

Central scheme

차분식에 완전해를 적용하면

\[ \frac{D_j^{n+1} + \epsilon_j^{n+1} - D_{j}^n - \epsilon_j^{n}}{\Delta t} + \frac{a (D_{j+1}^n + \epsilon_{j+1}^{n} - D_{j-1}^n - \epsilon_{j-1}^{n})}{2 \Delta x} = 0. \]

완전해는 차분식에 대한 오차가 없으므로,

\[ \frac{\epsilon_j^{n+1} - \epsilon_j^{n}}{\Delta t} + \frac{a (\epsilon_{j+1}^{n} - \epsilon_{j-1}^{n})}{2 \Delta x} = 0. \]

이 때 오차를 아래와 같이 표현하자.

\[ \epsilon_j^n = \sigma^n e^{ikx_j} \]

즉 오차는 공간에 대해 \(2 \pi / k\)의 주기를 갖는 형태이다. 이를 오차에 대한 차분식에 적용하면

\[ \frac{\sigma^{n+1} e^{ikx_j} - \sigma^n e^{ikx_j}}{\Delta t} + \frac{a (\sigma^n e^{ik(x_j + \Delta x)} - \sigma^n e^{ik(x_j - \Delta x)})}{2 \Delta x} = 0. \]

\(\sigma^n e^{ikx_j}\) 를 각 변에 나누어서 정리하면

\[ \sigma = 1 - \frac{a \Delta t}{\Delta x} (i \sin (k \Delta x)) \]

Central scheme은 \(|\sigma| > 1\) 이므로 오차가 증폭된다. 즉 불안정하다.

Upwind scheme

Upwind 차분식에 완전해를 적용하면

\[ \frac{D_j^{n+1} + \epsilon_j^{n+1} - D_{j}^n - \epsilon_j^{n}}{\Delta t} + \frac{a (D_{j}^n + \epsilon_{j}^{n} - D_{j-1}^n - \epsilon_{j-1}^{n})}{\Delta x} = 0. \]

오차에 대한 식은 다음과 같다.

\[ \frac{\epsilon_j^{n+1} - \epsilon_j^{n}}{\Delta t} + \frac{a (\epsilon_{j}^{n} - \epsilon_{j-1}^{n})}{\Delta x} = 0. \]

오차를 주기 형태로 표현해서 위 차분식에 적용하면

\[ \frac{\sigma^{n+1} e^{ikx_j} - \sigma^n e^{ikx_j}}{\Delta t} + \frac{a (\sigma^n e^{ik(x_j)} - \sigma^n e^{ik(x_j - \Delta x)})}{\Delta x} = 0. \]

\(\sigma^n e^{ikx_j}\) 를 각 변에 나누어서 정리하면

\[ \sigma = 1 - \frac{a \Delta t}{\Delta x} (1 - e^{-ik\Delta x}) = (1 - \nu + \nu \cos (k \Delta x)) - i \nu \sin (k \Delta x) \]

이때 \(\nu = a \Delta t / \Delta x\) 를 CFL 수라고 한다.

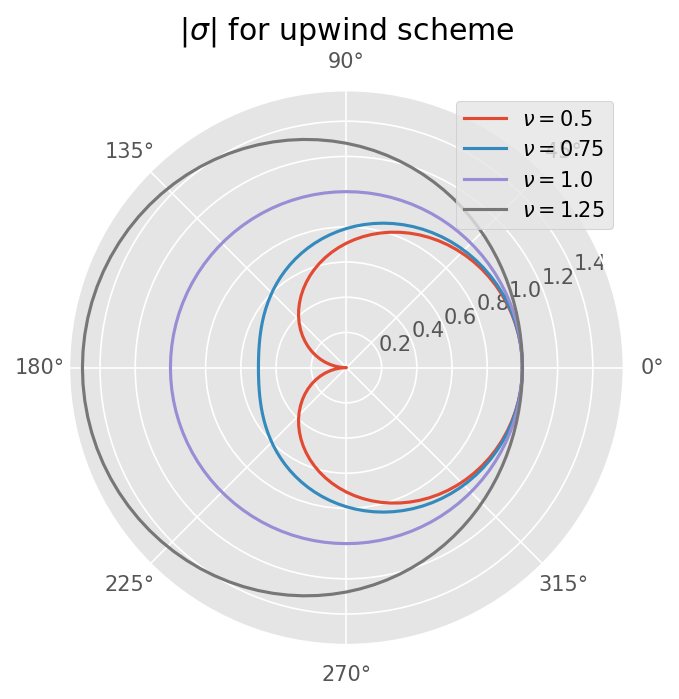
수치 기법이 안정적이려면 \(|\sigma| \le 1\) 이어야 한다. \(\nu\) 값을 다르게 하면서 \(|\sigma|\) 를 그려보면 아래와 같다. 이를 만족하려면 \(\nu \le 1\) 이다.

%matplotlib inline
from matplotlib import pyplot as plt

import numpy as np

plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150

theta = np.linspace(0, 2*np.pi, 101)
fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})

nus = [0.5, 0.75, 1.0, 1.25]
for nu in nus:
    sigma = 1 - nu *(1 - np.exp(-theta*1j))
    ax.plot(theta, abs(sigma))

ax.legend([r'$\nu={}$'.format(nu) for nu in nus])
ax.set_title(r'$|\sigma|$ for upwind scheme')

Text(0.5, 1.0, '$|\\sigma|$ for upwind scheme')

CFL condition 의미

CFL 조건 (\(\nu \leq 1\))의 물리적 의미는 수치적인 Domain of Dependence가 이론적인 Domain of Depence 보다 커야 한다. 즉 파동의 전파 특성을 계산 과정에서 충분히 반영할 수 있어야 한다.

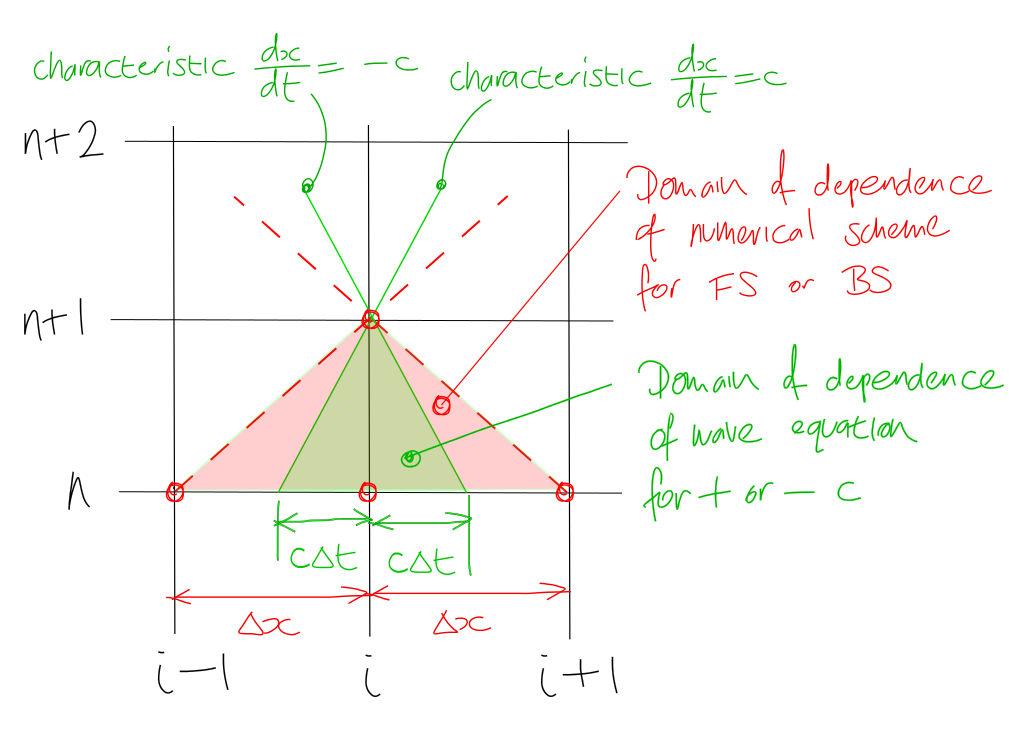
Fig. 9 Physical meaning of CFL condition (thevisualroom.com)

Convergence

수치적으로 구한 해가 완전해가 되려면 다음 두 조건을 만족해야 한다.

• Consistency : 격자와 시간 간격을 줄였을 때 차분식 (FDE)가 편미분 방정식 (PDE)을 근사해야 한다.

• Stability : 이론해와 차분해의 오차가 증폭되지 않아야 한다.

이 두 조건을 만족할 때 수치적으로 구한 해가 이론해를 수렴한다. (Lax theorem)

몇 가지 수치 기법

Lax Friedrich Scheme

Central 기법에서 시간 차분시 \(u_j^n\) 대신 평균값 \((u_{j+1}^n + u_{j-1}^n)/2\) 을 넣는다.

\[ u_j^{n+1} = \frac{u_{j+1}^n + u_{j-1}^n}{2} - \frac{a \Delta t}{2 \Delta x} (u_{j+1}^n - u_{j-1}^n). \]

Lax Wendroff Scheme

\(n+1\) 시간에서 Taylor expansion을 활용하면

\[ u_j^{n+1} = u_j^n + u_t \Delta t+ \frac{1}{2!} u_{tt} \Delta t^2 + O(\Delta t^3) \]

Wave equation 식을 이용해서 \(u_t\), \(u_{tt}\) 는 다음과 같이 근사할 수 있다.

\[\begin{split} u_t = -a u_x \\ u_{tt} = a^2 u_{xx} \end{split}\]

이를 적용하면

\[ u_j^{n+1} = u_j^n - a \Delta t u_x + \frac{1}{2} a^2 \Delta t^2 u_{xx} + O(\Delta t^3) \]

중앙 차분을 적용하면 다음과 같다.

\[ u_j^{n+1} = u_j^n - \frac{a \Delta t}{2 \Delta x} (u_{j+1}^n - u_{j-1}^n) + \frac{a^2 \Delta t^2}{2 \Delta x^2} (u_{j+1}^n -2 u_j^n + u_{j-1}^n) \]

실습

• Lax Friedrich, Lax Wendroff 기법의 정확도를 Taylor expansion을 이용해서 분석해보고 Consistency 에 대해 논의하시오.

• Lax Friedrich 기법에 대해 von Neumann 안정성 분석을 수행하시오.

• \(N\) = 50 일 때 Upwind, Central, Lax Friedrich, Lax Wendroff 기법에 대해서 Sine Wave 문제를 해석하시오, \(CFL\) 수는 0.5, 0.9, 1.5. 2.0 에 대해서 수행하시오.

• (Optional) Lax Wendroff 기법에 대해 von Neumann 안정성을 분석하시오.